引言
之前学习的 critical point,在训练任务中并不是做大的障碍,也不是非常常见。也就是说,训练受阻,并不一定是梯度太小,还可能是别的原因。
1 Training stuck ≠ Small Gradient
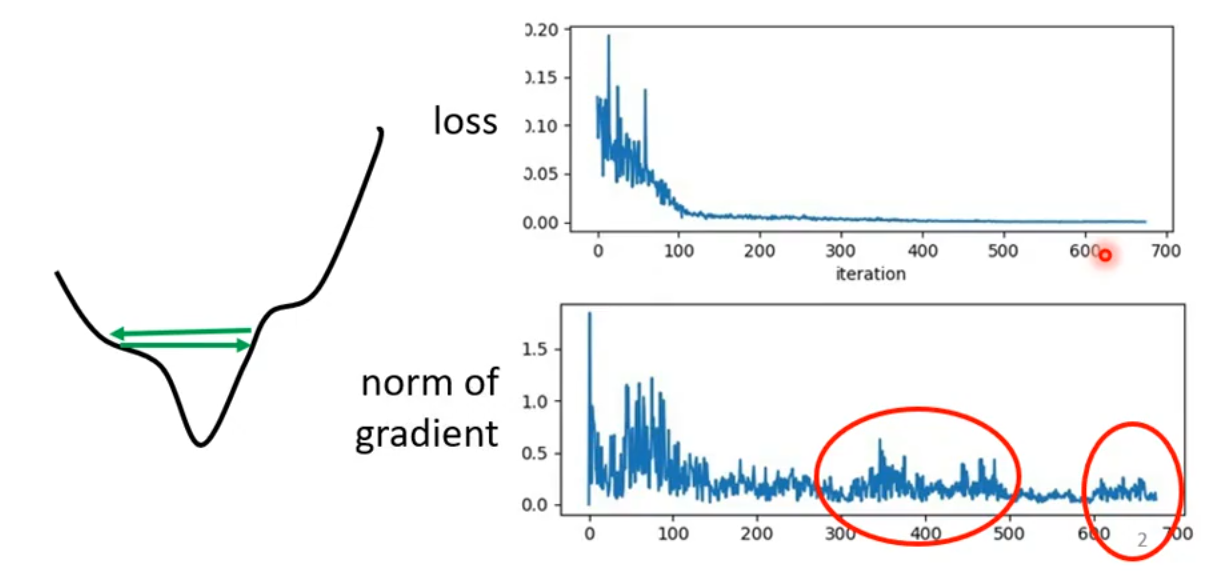
Grad Norm(也称为 Norm of Gradient):梯度范数,是梯度动态的量化,梯度范数反映参数更新步长的大小,直接影响优化过程的稳定性。
我们来看上面这张图,随着迭代的次数增加,loss趋于平缓不再下降。但是随着迭代的次数增加,梯度并不是趋于0的,而是在跳动。这说明此时训练停滞时(即loss趋于平缓),并不是因为 critical point (即梯度趋于0),而是别的原因。
由于梯度在上下跳动,很可能训练过程碰见了loss函数的“山谷”,梯度在山谷之间来回折返。
2 Learning Rate的影响
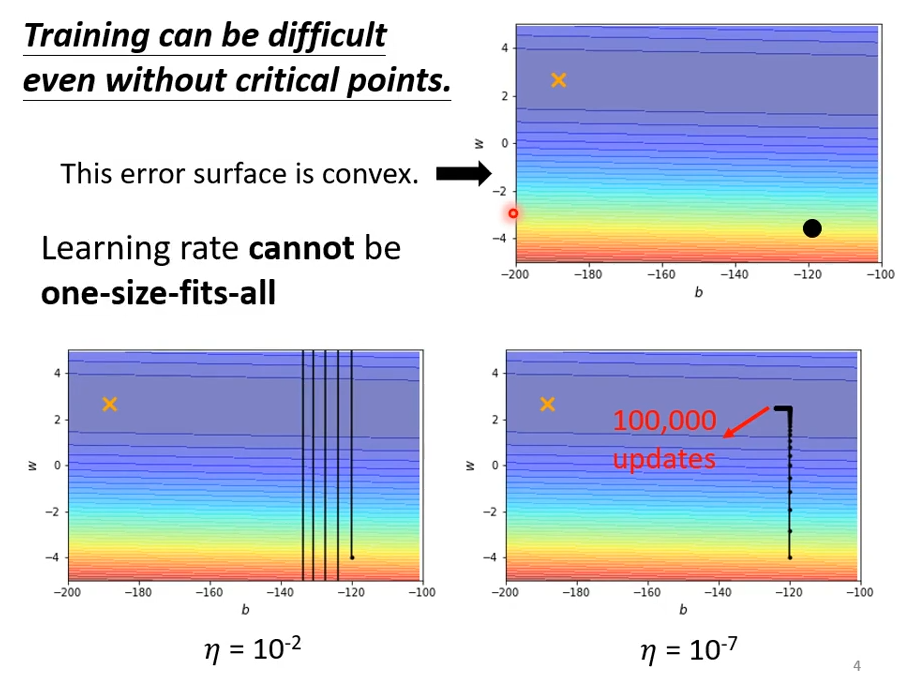
上面的图片中,error surface就是loss曲线,convex(凸的)即曲线只有一个碗状的谷底,没有坑坑洼洼的小盆地,也没有马鞍。可以将红色部分看作高地,颜色越灰地势越低。
当学习率为\eta = 10^{-2}时,由于学习率太大,梯度在上下大幅度跳动,无法收敛到loss较低的地方;当学习率\eta = 10^{-7}时,由于学习率很小,成功让loss收敛得越来越小,但是在后半段灰色部分,由于曲线非常平缓,而学习率又很小,所以收敛速度非常慢,很难达到loss最小值。
由此我们发现,在训练的不同时候,我们需要不同大小的Learning Rate。
在陡峭的地方,需要小的学习率;
在平缓的地方,需要大的学习率。
即对于不同的梯度,需要不同大小的学习率;
梯度是对某一组参数计算出来的,也即对于不同的参数,需要不同大小的学习率。
3 优化 Learning Rate:\eta \rightarrow \frac{\eta}{\sigma_i^t}
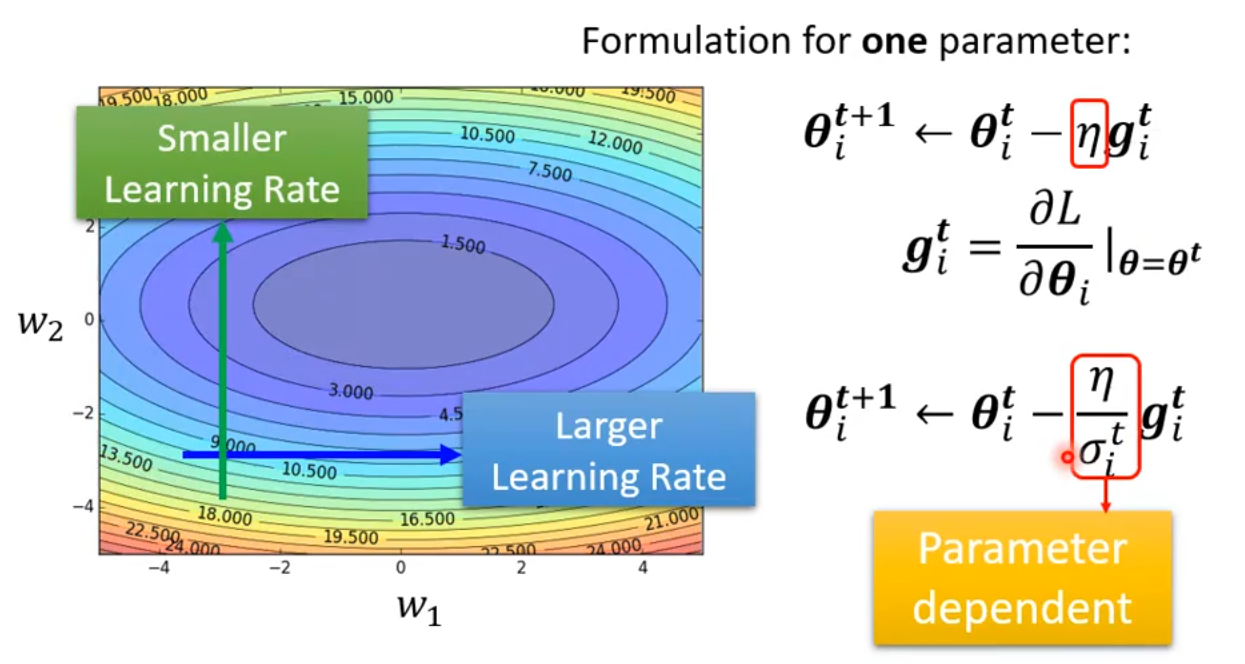
我们原先使用梯度下降进行更新参数时,使用的方法是:为了简单起见,我们只看一个参数,即在第i个参数\boldsymbol \theta_i。在第t+1轮更新参数时,\boldsymbol \theta_i^{t+1} \leftarrow \boldsymbol \theta_i^t - \eta \boldsymbol g_i^t,其中\boldsymbol g_i^t = \frac{\partial L}{\partial \boldsymbol \theta_i}|_{\boldsymbol \theta = \boldsymbol \theta^t}。
现在我们需要调整这个更新参数的过程,引入可调节的学习率\frac{\eta}{\sigma_i^t}。
更新过程变成:\boldsymbol \theta_i^{t+1} \leftarrow \boldsymbol \theta_i^t - \frac{\eta}{\sigma_i^t} \boldsymbol g_i^t。也就是将原来的学习率\eta变成了可变化的学习率\frac{\eta}{\sigma_i^t}。其中\sigma_i^t是一个依赖于i和t的值,它是在不断变化的,接下来讲解变化的方法。
3.1 Root Mean Square
参数更新:
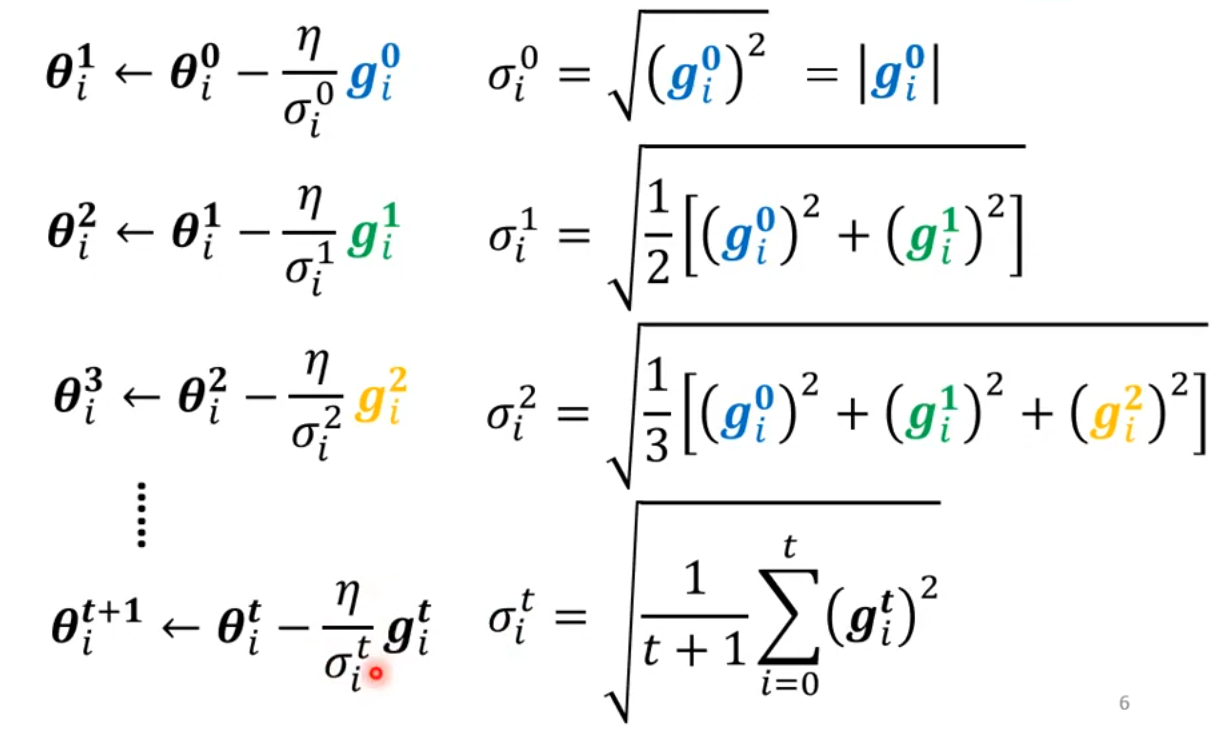
梯度越小,学习率就会变得越高,参数的更新的step就越大;
梯度越大,学习率就会变得越低,参数的更新的step就越小。
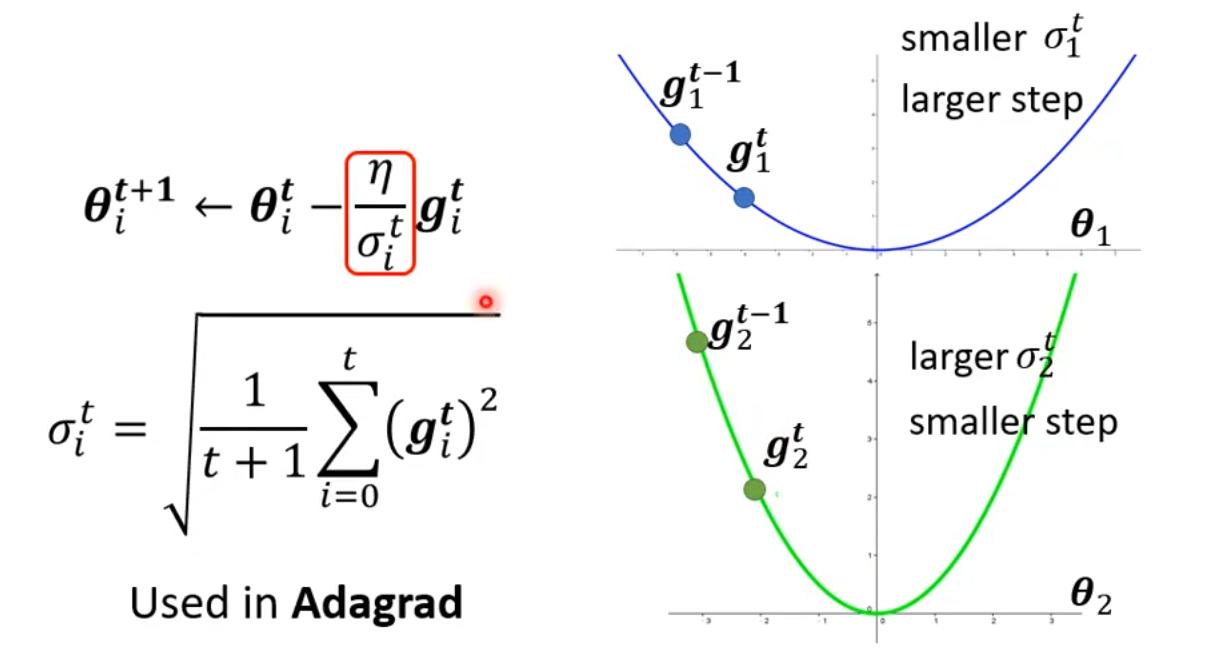
Adagrad(Adaptive Gradient)是一种自适应学习率的优化算法,2011年由 Duchi 等人提出。对每个参数使用不同的学习率,频繁出现的梯度方向用小步长,罕见方向用大步长。
优点:在稀疏数据(如 NLP、推荐系统)上表现好。
缺点:学习率单调递减,训练后期可能过小,提前“停滞”;内存需要保存累积平方梯度,参数多时显存占用高。
3.2 RMSProp
参数更新:
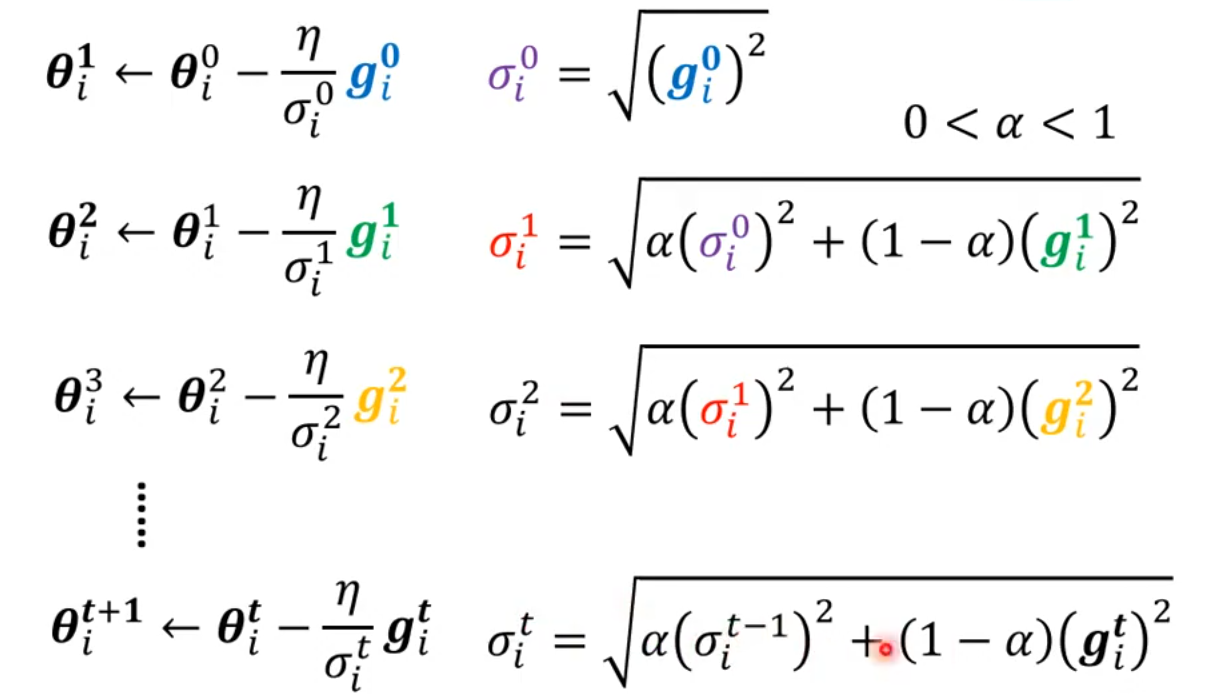
其中\alpha的取值在0到1之间,它是一个超参数。它可以解释为当前计算的梯度的重要程度,\alpha越小,则1 - \alpha越大,则当前计算的梯度\boldsymbol g_i的重要性占比就越高。

在实际的训练任务中,我们在 Optimization 的时候,用到的优化方法是 Adam。这个优化方法结合了 RMSProp 和 Momentum。参考论文为:ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION。

4 Learning Rate Scheduling
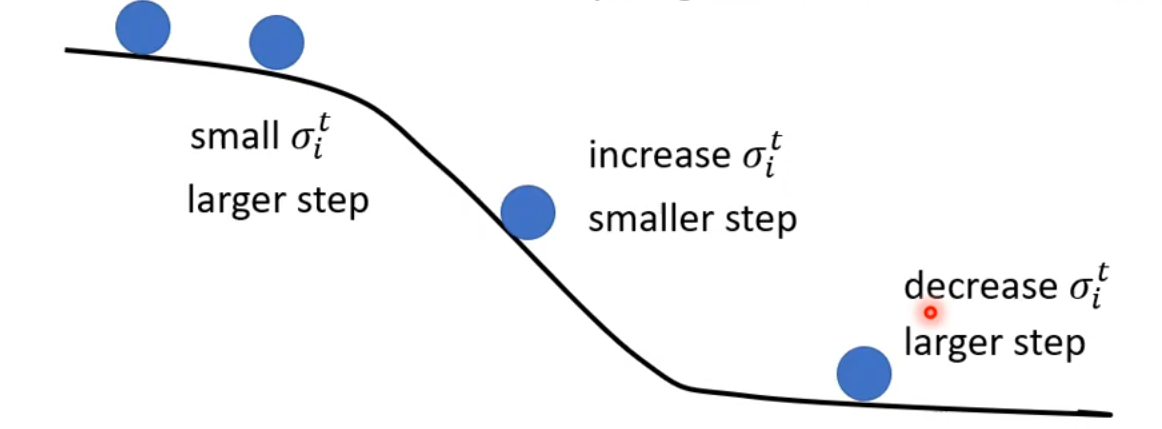
使用 Root Mean Square 方法后,学习率的变更为\eta \rightarrow \frac{\eta}{\sigma_i^t}。在训练中发现,在训练的后期,在平缓的地方,出现了突然波动的现象,波动过后会逐渐收敛回来。
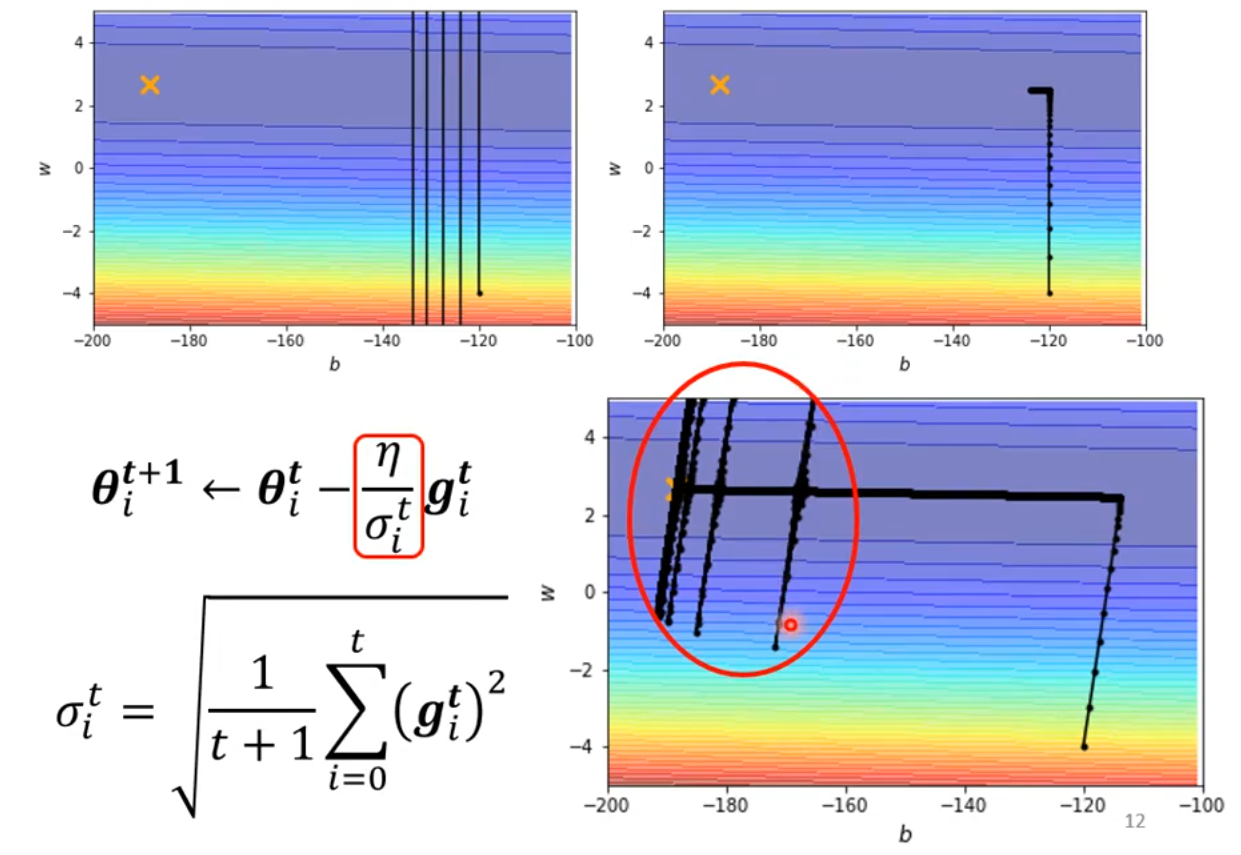
为了解决这个问题,引入 Learning Rate Scheduling,将原本的\eta常数,换成与时间相关的函数\eta^t,这里的t指的是时间:
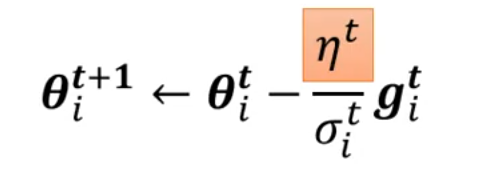
4.1 Learning Rate Decay
随着训练的推进,我们越来越靠近最终目标,所以我们应该逐渐降低学习率,所以\eta^t可以是一个随着t增减而减小的函数:

4.2 Warm Up
初始的时候,\sigma_i^t的方差还很大,这个时候使用较大的学习率可能会影响训练,所以可以在前期慢慢从小到大增加学习率,到某个时刻再逐渐较小。

可以参考 RAdam 的论文,有更多对 Warm Up 的解释。
5 对 Optimization 的总结
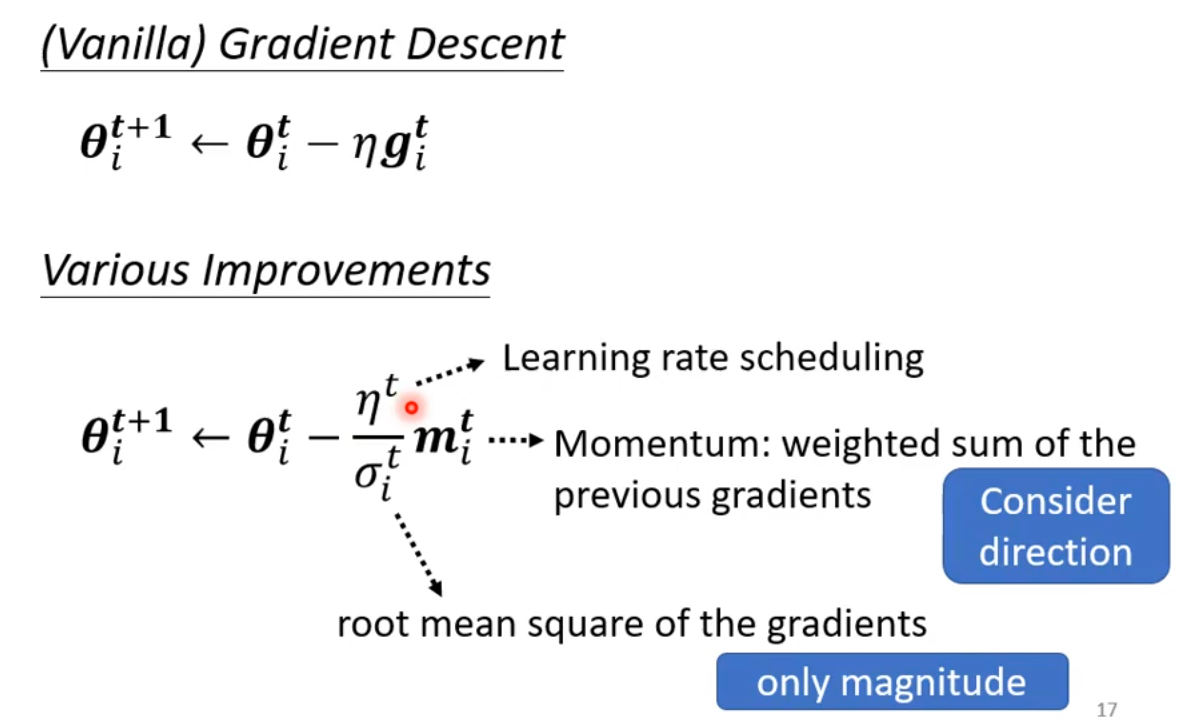
Vanilla的意思是最原始的方法。
总之对 Optimization 的各种优化方式,无外乎三个方面:
Learning Rate Scheduling
Momentum
\sigma_i^t,有 Root Mean Square、RMSProp
其中 Momentum 考虑梯度大小和参数更新的方向,\sigma_i^t考虑梯度的大小。


评论区